Super Agents of AI

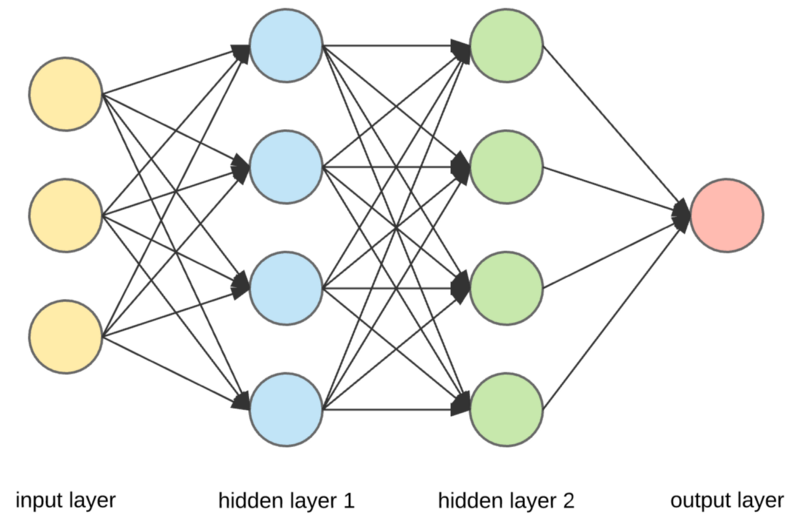
Structures of Neural Networks

• Input layer
• Hidden layer
• Output layer

Activation Function

1. Sigmoid

   $$ F(x) = \frac{1}{1+e^{-x}} $$

2. Relu

   $$ F(x) = \max(0,x) $$

Summary

• A set of nodes, analogous to neurons, organized in layers.
• A set of weights representing the connections between each neural network layer and the layer beneath it. The layer beneath may be another neural network layer, or some other kind of layer.
• A set of biases, one for each node.
• An activation function that transforms the output of each node in a layer. Different layers may have different activation functions.

Training Neural Nets

Back Propagation

• Gradients are important.
• Gradients can vanish.
  • Each additional layer can successively reduce signal vs. noise.
  • Relu is useful here.
• Gradients can explode.
  • Learning rates are important here.
  • Batch normalization (useful knob) can help.
• Relu layers can die.
  • Lowering the learning rate can help keep Relu units from dying.

Normalizing the Values

• Roughly zero-centered, [-1,1] range often works well.
• Helps gradient descent converge, avoid NaN trap.
• Avoiding outlier values can also help.
• Linear scaling.

def linear_scale(series):
    min_val = series.min()
    max_val = series.max()
    scale = (max_val - min_val) / 2.0
    return series.apply(lambda x:((x - min_val) / scale) - 1.0)

• Hard cap (clipping) to max, min.

def clip(series, clip_to_min, clip_to_max):
    return series.apply(lambda x:(min(max(x, clip_to_min), clip_to_max)))

• Z score normalize

def z_score_normalize(series):
    mean = series.mean()
    std_dv = series.std()
    return series.apply(lambda x:(x - mean) / std_dv)

• Log scaling.

def log_normalize(series):
    return series.apply(lambda x:math.log(x+1.0))

Dropout Regularization

• It’s another form of regularization for NNs.
• Works by randomly “dropping out” units in a network for a single gradient step.
• The more you drop out, the stronger the regularization.
• 0.0 = no dropout regularization.
• 1.0 = drop everything out! learns nothing.
• Intermediate value (0, 1) is more useful.

Note: Cover Picture